За допомогою програми GeoGebra можна будувати кривi, попередньо склавши параметричне рiвняння:
-
Якщо потрiбно скласти параметричне рiвняння прямої, тобi знадобиться Пункт 4. Пiсля складання параметричного рiвняння пряма буде побудована автоматично.
-
Якщо потрiбно побудувати кривi на площинi, тобi знадобиться Пункт 3.
-
Якщо ти бажаєш побудувати кривi у просторi, тобi знадобиться Пункт 2.
Iнструкцiя GeoGebra 1
Складання параметричного рiвняння прямої
- 1.
- Вiдкрий види
Полотно 3DтаАлгебрапiд вкладкоюВидуМеню. - 2.
- Якщо дано вектор напряму, введи його у видi
Алгебраза допомогою командиВектор(Точка),
щоб команда спрацювала пiд час наступних етапiв. Запиши iм’я вектора у видi
Алгебра, оскiльки воно знадобиться пiзнiше. - 3.
- Залежно вiд наданої iнформацiї виконай такi дiї у видi
Алгебра:-
Якщо дано точку та вектор напряму, введи команду
Пряма(Точка, Вектор напряму)
та встав у полi
Точкасвою точку, а в полiВектор напрямуiм’я вектора з етапу 2. -
Якщо дано двi точки введи команду
Пряма(Точка, Точка)
та в обидвох полях
Точкавстав координати кожної зi своїх точок.
Пiсля цього у видi
Полотно 3Dз’явиться пряма. Параметричне рiвняння також з’явиться у видiАлгебра.Зверни увагу! У програмi
GeoGebraдля позначення параметра використовується грецька лiтера , замiсть звичної . -
- 4.
- Щоб обернути рисунок в
Полотно 3D, натисни на iнструментОбертання 3D графiки.
Приклад 1
Склади параметричне рiвняння прямої, що проходить через точку
з вектором напряму
Дотримуючись наведеної вище Пункт 4, введемо команду
Пряма(Точка, Вектор напряму)
в окремому рядку виду Алгебра . Потiм введемо команду
Пряма(Точка, Вектор напряму)
та замiнимо поле Точка на (5, -6, 7), а поле Вектор напряму на iм’я вектора. Пiсля цього отримаємо таке параметричне рiвняння
Приклад 2
Склади параметричне рiвняння прямої, що проходить через точки
and
Дотримуючись наведеної вище Пункт 4, введемо команду
Пряма(Точка, Точка)
та замiнимо перше поле Точка на (-3, 5, -4), а друге поле Точка на (-1, -1, -1). Пiсля цього отримаємо таке параметричне рiвняння
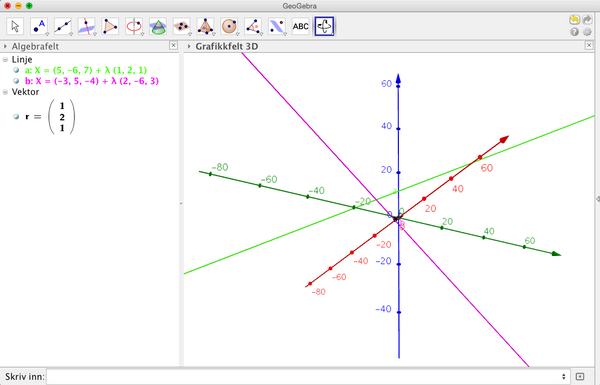
Iнструкцiя GeoGebra 2
Побудова кривої на площинi за допомогою параметричних рiвнянь
- 1.
- Вiдкрий види
АлгебратаПолотнопiд вкладкоюВидуМеню. - 2.
- Використай команду
Крива(Вираз, Вираз, Параметр, Початкове значення, Кiнцеве значення)
у видi
Алгебра. Переконайся, що ти використовуєш версiю, де є два поляВираз(є ще одна версiя з трьома такими полями). - 3.
- Введи вирази та —саме в такому порядку—в поля
Вираз. Введи в полеПараметр, зазнач початкове й кiнцеве значення для у вiдповiдно поляхПочаткове значеннятаКiнцеве значення. Натисни клавiшуEnter.Пiсля цього твоя крива з’явиться у видi
Полотно. Крiм того, параметричне рiвняння кривої з’явиться у видiАлгебра.
Приклад 3
Побудуй криву, заданої такими параметричними рiвняннями
та
з 0 як початковим значенням i 50 як кiнцевим значенням параметра .
Дотримуючись наведеної вище Пункт 3, використаємо команду
Крива(Вираз, Вираз, Параметр, Початкове значення, Кiнцеве значення),
замiнивши
-
Перше поле
Виразна3t -
Друге поле
Виразнаt+4 -
Поле
Параметрнаt -
Поле
Початкове значенняна0 -
Поле
Кiнцеве значенняна50
Опiсля плоска крива з’явиться у видi Полотно , а параметричнi рiвняння — у видi Алгебра .
Iнструкцiя GeoGebra 3
Побудова кривої в просторi за допомогою параметричних рiвнянь
- 1.
- Вiдкрий види
АлгебратаПолотно 3Dпiд вкладкоюВидуМеню. - 2.
- У видi
Алгебравведи командуКрива(Вираз, Вираз, Вираз, Параметр, Початкове значення, Кiнцеве значення)
in
Алгебра. Переконайся, що ти використовуєш версiю команди, що має три поляВираз(є ще одна версiя з двома такими полями). Введи вирази для , та , саме в такому порядку, в поляВираз. Введи в полуПараметр, та зазнач початкове й кiнцеве значення для у вiдповiдно поляхПочаткове значеннятаКiнцеве значення. Натисни клавiшуEnter.Пiсля цього твоя крива з’явиться у видi
Полотно 3D. Крiм того, параметричне рiвняння кривої з’явиться у видiАлгебра.Щоб змiнити проєкцiю у видi
Полотно 3D, обери iнструментОбертання 3D графiкиi скористайся курсором, щоб змiнити проєкцiю на свiй смак.
Приклад 4
Побудуй криву, задану такими параметричними рiвняннями
та
з 0 як початковим значенням i 100 як кiнцевим значенням параметра .
Дотримуючись наведеної вище Пункт 3, вводимо команду
Крива(Вираз, Вираз, Вираз, Вираз, Параметр, Початкове значення, Кiнцеве значення)
замiнивши
-
Перше поле
Виразнаt -
Друге поле
Виразна-2t+1 -
Третє поле
Виразнаt+2 -
Параметрwitht -
Поле
Початкове значенняна0 -
Кiнцеве значенняна100
Опiсля об’ємна крива з’явиться у видi Полотно , а параметричнi рiвняння — у видi Алгебра .







